内積を求める計算式
内積(ドット積)とは、2つのベクトルa・ベクトルbにおいて以下の式で求められる値です。
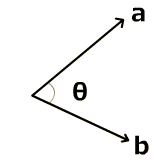a・b = |a||b|cosθ
a・b は「ベクトルaとベクトルbの内積」を表す式で、|a|はベクトルaの大きさ、|b|はベクトルbの大きさ、そしてθはベクトルaとベクトルbが成す角を表しています。
また、2次元ベクトルa(ax,ay)・ベクトルb(bx,by)として
a・b = |a||b|cosθ
また、2次元ベクトルa(ax,ay)・ベクトルb(bx,by)として
a・b = (ax × bx) + (ay × by)
3次元ベクトルa(ax,ay,az)・ベクトルb(bx,by,bz)として
a・b = (ax × bx) + (ay × by) + (az × bz)
といった式でも求めることができます。
[例] 2次元ベクトル(120,10)と(20,180)の内積を求める
= (120 × 20) + (10 × 180)
= 2400 + 1800
= 4200
よって、2つのベクトルの内積は4200
= 2400 + 1800
= 4200
よって、2つのベクトルの内積は4200
計算機の使い方
まず最初に、上の入力欄に内積を求める2つのベクトルを入力します。
3次元ベクトルの場合はX・Y・Zの3つ、2次元ベクトルの場合はX・Yのみ入力してZは0のままでOkです。
ベクトルの入力が終わったら「ベクトルの内積を計算」ボタンを押してください。
すると、下の欄に内積が表示されます。
3次元ベクトルの場合はX・Y・Zの3つ、2次元ベクトルの場合はX・Yのみ入力してZは0のままでOkです。
ベクトルの入力が終わったら「ベクトルの内積を計算」ボタンを押してください。
すると、下の欄に内積が表示されます。
関連コンテンツ
入力された角度から正弦(sin)・余弦(cos)・正接(tan)の値を求めるツール。
三角関数の意味と使い方の解説付き。
三角関数の意味と使い方の解説付き。
2次元ベクトル・3次元ベクトルの大きさ(長さ)を求めるための計算式の解説と計算ツール。