ベクトルの大きさ(長さ)を求める方法
ベクトルの大きさ(長さ)は、「ピタゴラスの定理」を使うことによって求めることができます。
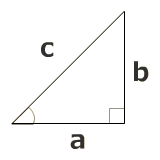
ピタゴラスの定理(三平方の定理)

左の図のような直角三角形の3つの辺の長さについて
a² + b² = c²
が成り立つ。
a² + b² = c²
が成り立つ。
2次元ベクトルの大きさを求める式
2次元ベクトル(x,y)の場合は、ピタゴラスの定理で簡単に大きさを求めることができます。
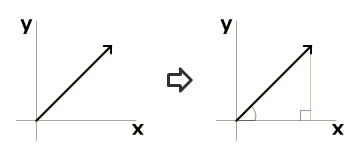

2次元ベクトル(x,y)の大きさ = √x² + y²
[例] 2次元ベクトル(120,80)の大きさ(長さ)を求める
= √120² + 80²
= √14400 + 6400
= √20800
= 144.222...
よって、2次元ベクトル(120,80)の大きさ(長さ)は
約144
= √14400 + 6400
= √20800
= 144.222...
よって、2次元ベクトル(120,80)の大きさ(長さ)は
約144
3次元ベクトルの大きさを求める式
3次元ベクトル(x,y,z)の場合は一旦zを置いておいて、まずxとyのみで2次元ベクトルの大きさを求めます。
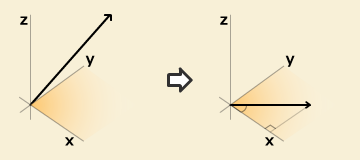
そして、上記の計算で得られた2次元ベクトルの大きさとzを使って最終的なベクトルの大きさを求めます。
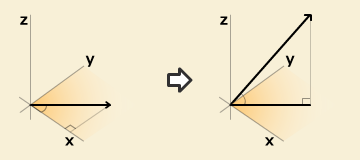

2次元ベクトル(x,y)の大きさ = √x² + y²
そして、上記の計算で得られた2次元ベクトルの大きさとzを使って最終的なベクトルの大きさを求めます。

| 3次元ベクトル(x,y,z)の大きさ |
= √2次元ベクトル(x,y)の大きさの二乗 + z² |
|
= √x² + y² + z² |
[例] 3次元ベクトル(120,80,30)の大きさ(長さ)を求める
最初にxとyの2次元ベクトルの大きさを求める。
= √120² + 80²
= √14400 + 6400
= √20800
= 144.222...
続いて求められたベクトルの大きさとz値で最終的なベクトルの大きさを求める。
= √144.222² + 30²
= √20800 + 900
= √21700
= 147.3091...
よって、3次元ベクトル(120,80,30)の大きさ(長さ)は
約147
= √120² + 80²
= √14400 + 6400
= √20800
= 144.222...
続いて求められたベクトルの大きさとz値で最終的なベクトルの大きさを求める。
= √144.222² + 30²
= √20800 + 900
= √21700
= 147.3091...
よって、3次元ベクトル(120,80,30)の大きさ(長さ)は
約147
計算機の使い方
WEBブラウザ上で動作する、ベクトルの大きさ(長さ)を計算するツールです。
上の入力欄に大きさを求めたいベクトルの値を入力して中段のボタンを押すと、下の欄にベクトルの大きさが表示されます。
上の入力欄に大きさを求めたいベクトルの値を入力して中段のボタンを押すと、下の欄にベクトルの大きさが表示されます。